Introducing hoc1: A simple calculator

This initial version of hoc implements a tiny REPL (Read-Evaluate-Print Loop), and contains only the 4 basic arithmetic operations: addition, subtraction, multiplication, and division. It does understand operator precedence and parentheses, so multiplication/division are applied before addition/subtraction, unless parenthesized.

> ./hoc1
1+2
        3
1+3*4
        13
(1+3)*4
        16
10/3
        3.333333
1/0
        inf

But for this simple version, that’s approximately where “understanding” ends; hoc1 doesn’t even understand negative numbers. Further, upon encountering an error, it simply exits.

> ./hoc1
-3
./hoc1: syntax error (on line 1)
>

Still, this is enough for us to begin building one of the major components of hoc that lasts all the way to the final version: its parser.

Running hoc1 Yourself

You’ll need:

• A C compiler
• make; almost any version should work; this stuff is based on 40-year old software
• A copy of GNU bison or another yacc-compatible parser generator. If you’re missing anything, this is it! For macOS, that’s just brew install bison or port install bison; for Linux or BSD, it should be part of every distribution’s package system.

Once you’ve got those installed, you can either copy/paste the Makefile on this page to build it, or download the hoc repository and run make hoc1 or make run-hoc1

Just Enough Parsing

• If you’re already familiar with shift-reduce parsing, but not yacc, you can skip to the yacc introduction.

• If you’re already familiar with yacc, you can probably just skim the code for hoc1 and move to hoc2.

A parser’s job is to recognize strings from a predefined language. Along the way, we would like it to produce some useful result or side effect.

Context-Free Languages

Obviously, some languages are simpler than others; we actually classify languages based on how hard it is to write the rules that describe it. For hoc, we’re interested in languages whose rules can be described with a context-free grammar (cleverly named context-free languages).

To describe a language with a context free grammar, we need to know:

1. The vocabulary of our language; that is, the list of strings that have meaning outside of our rules at all. These are called the tokens, or terminal symbols of our langauge.

2. Some rules about how those tokens can be combined together, called productions. Every production describes how we can combine symbols together to create a new, compound symbol. We call these non-terminal symbols.

3. Finally, we have to designate one of our symbols as the start symbol. The start symbol represents our “goal state”—if we match the rule for our start symbol, we’ve got a complete object.

   For example, an English-language parser might use sentence as its start symbol. If it did, then it would not accept input such as

   They became friends with

   Each word makes sense, but together they do not form a complete sentence.

   For a interactively-evaluated language like hoc, our start symbol will be something like “zero or more executable statements”.

A First Example: Addition Expressions

Consider a grammar to parse addition expressions.

Step 1. Define Tokens

What might the tokens of our language be? Well, certainly numbers seem like the basic ‘words’ of an addition operation.¹ We also can’t add without a plus sign, so:

Tokens: NUMBER and +.

We don’t need a name for the plus sign, since it’s only one character. We always write single-character tokens wrapped in single-quotes, and longer tokens as all-capitalized names.

Step 2: Write our rules

Now, let’s define our expressions. We’ll say that we can either have a single number, or an addition.

expr:     NUMBER
       |  sum
sum:      NUMBER '+' NUMBER

And this is a complete context-free grammar to recognize strings like: 42 or 4 + 2.

Parse Trees

It often helps, when discussing a given string, to examine how the input tokens eventually compose into the start symbol. One tool for showing this structure is a parse tree. Here are the parse trees for the two expressions mentioned above.

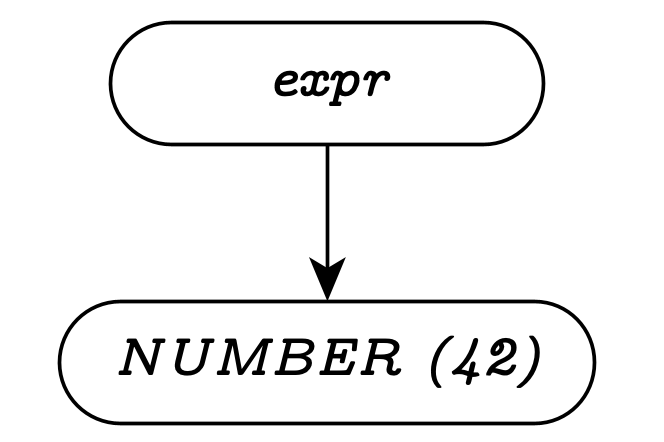
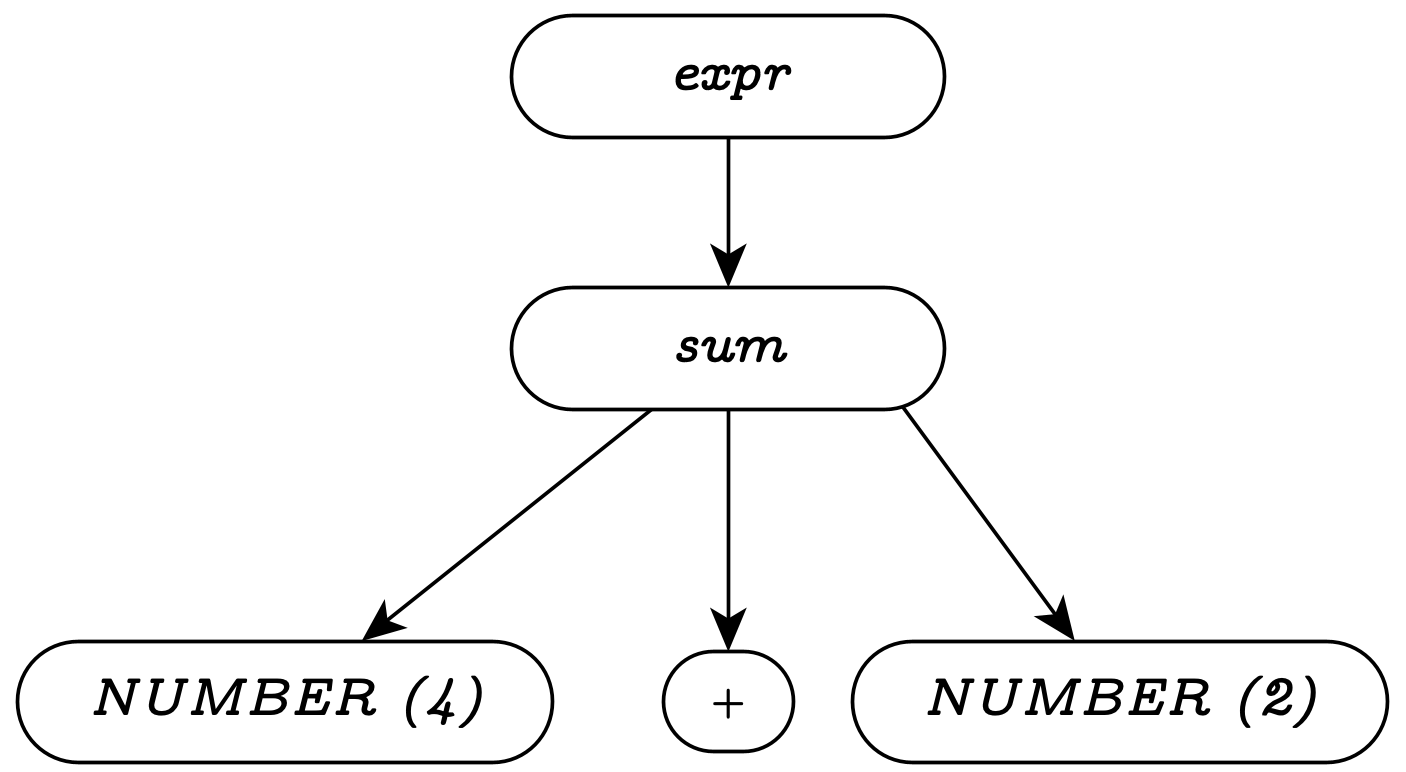
Handling Lists

Often, we’ll need to represent language constructs that allow a symbol to be repeated. Examples include function parameters, statements in a loop, etc. Our context-free grammars support this, via recursive nonterminals. A recursive nonterminal symbol uses itself within its definition.

As an example, let’s add support for arbitrary-length addition expressions to our example grammar:

expr:     NUMBER
       |  sum

sum:      NUMBER '+' NUMBER

To add support for sums with more than two operands, we can change the first operand to allow either a number, or another sum. We already have a construct for this idea: the expr nonterminal.

expr:     NUMBER
       |  sum

sum:      expr '+' NUMBER

This manner of recursion, where the recursive symbol appears first in the production, is called left-recursion. While both types of recursion are possible, left-recursion is more common, because it creates rules with left-associative operations, which often match our expectations for programming. (Almost all mathematical operations are left-associative)

Let’s examine a parse tree for 2+4+6+8 using this grammar:

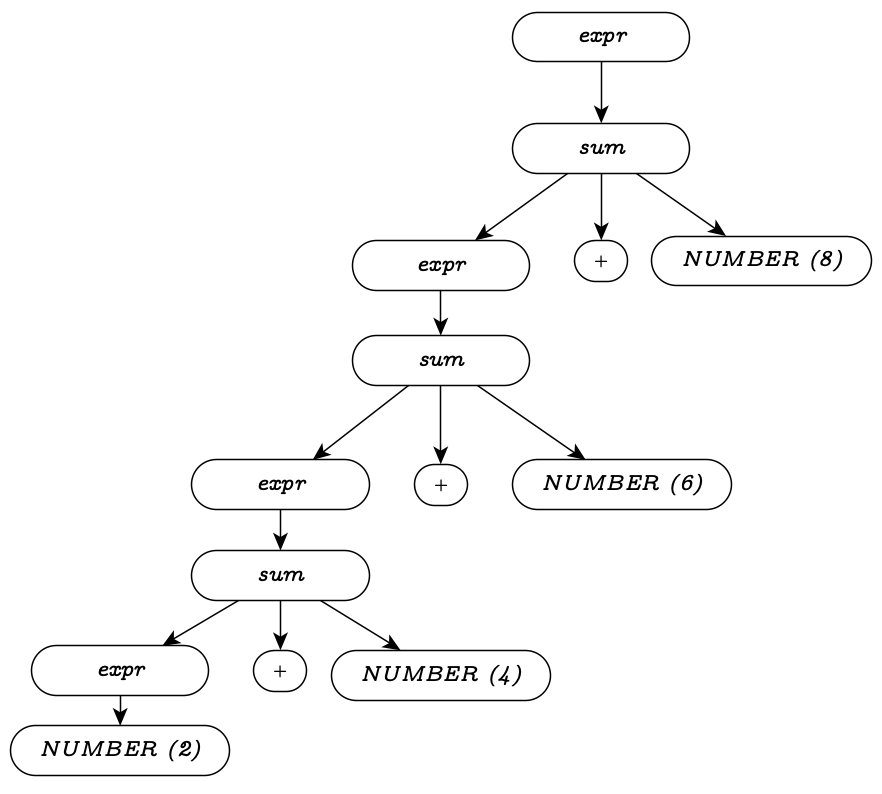
Ambiguity and Precedence

Another important detail that arises often is representing precedence of various operators; this is especially true when building an expression grammar, like the one we’ll need for hoc’s arithmetic. Precedence of operators is important for avoiding ambiguous grammars: grammars that permit multiple valid representations of the same input string.

To see the difficulty ambiguity creates, let’s add yet another feature to our running example: multiplication. Our first try will add a prod nonterminal to our grammar, much like sum.

expr:     NUMBER
       |  sum
       |  prod

sum:      expr '+' NUMBER

prod:     expr '*' NUMBER

This grammar is not ambiguous, but unfortunately, it’s also wrong; because both sum and prod must end with NUMBER, we cannot represent the correct grouping of “1 + prod”.

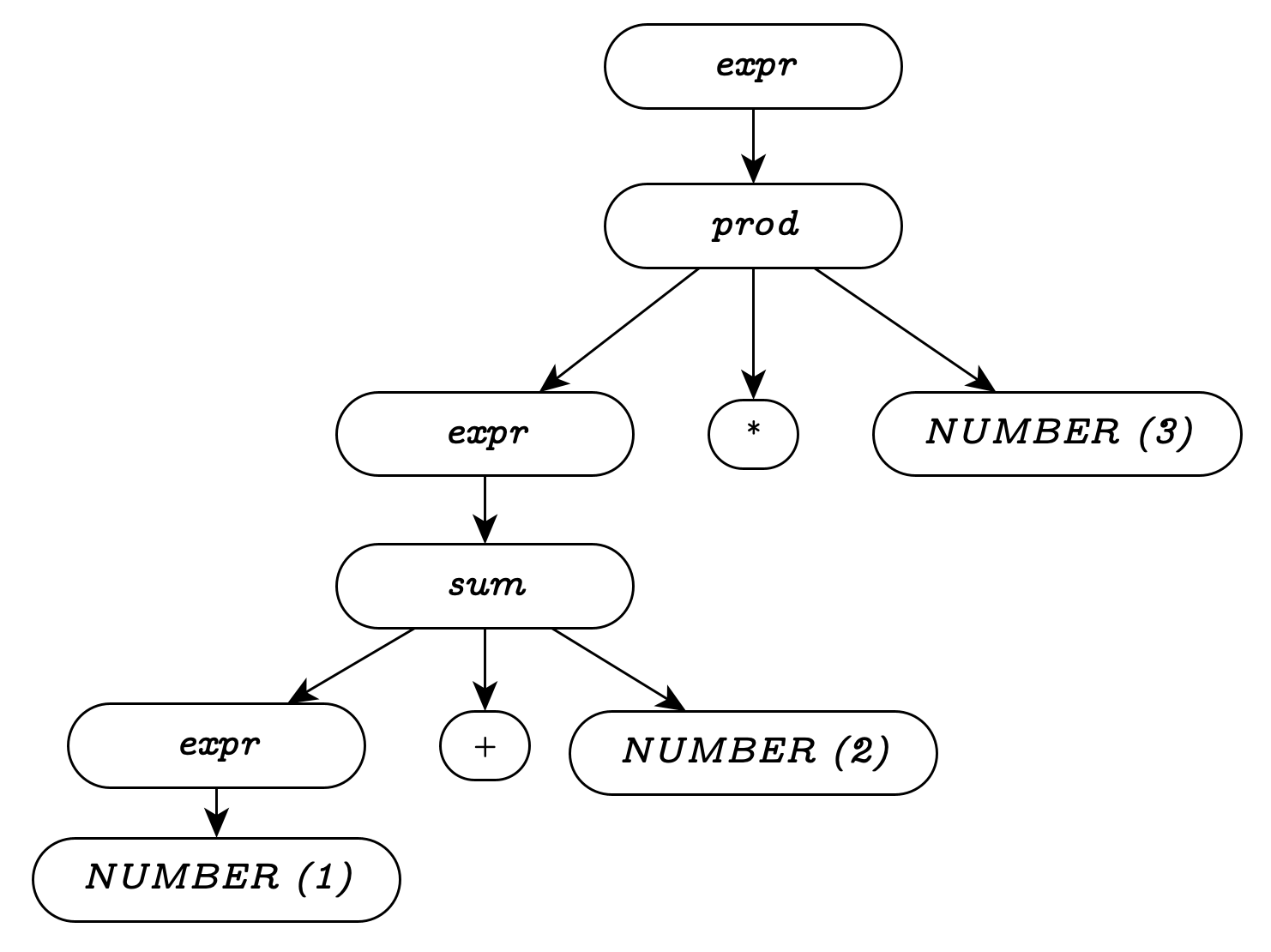
Let’s make the grammar more flexible, allowing recursion on either side:

expr:     NUMBER
       |  sum
       |  prod

sum:      expr '+' expr

prod:     expr '*' expr

We can definitely construct a parse tree with the correct grouping using this grammar:

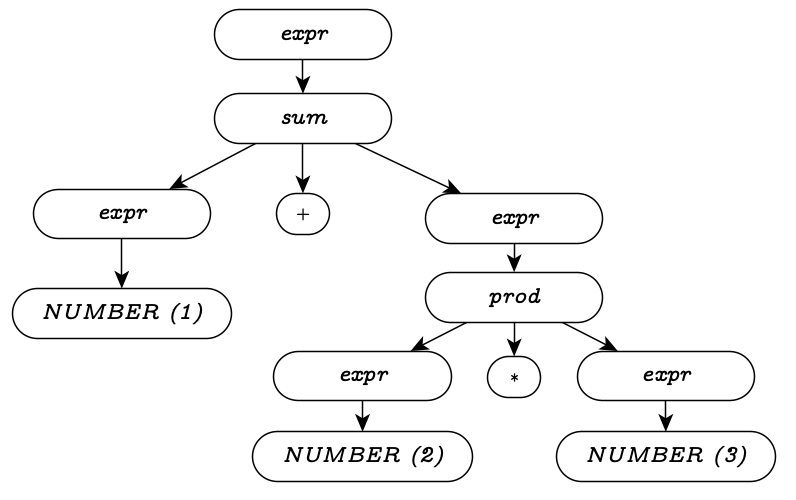
The problem is that this isn’t the only valid tree. Another valid tree for the same input string is below; which tree we get depends on which side of the tree we decide to place 2 on.

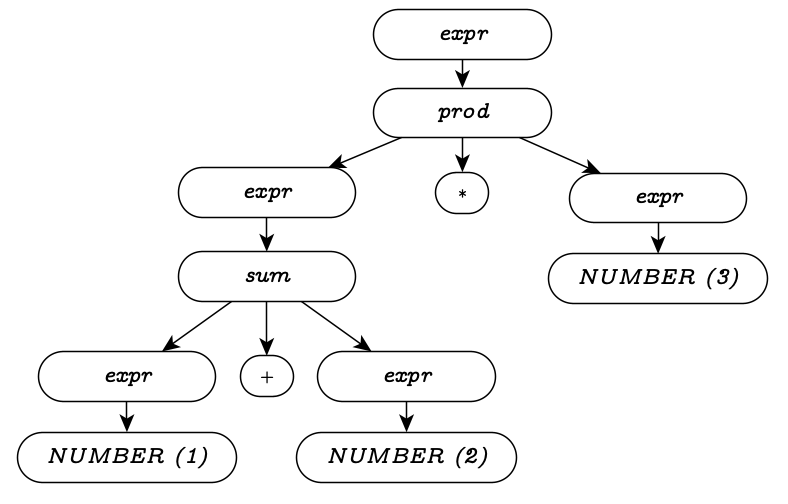
When a grammar can generate multiple parse trees for the same input string, it’s an ambiguous grammar.

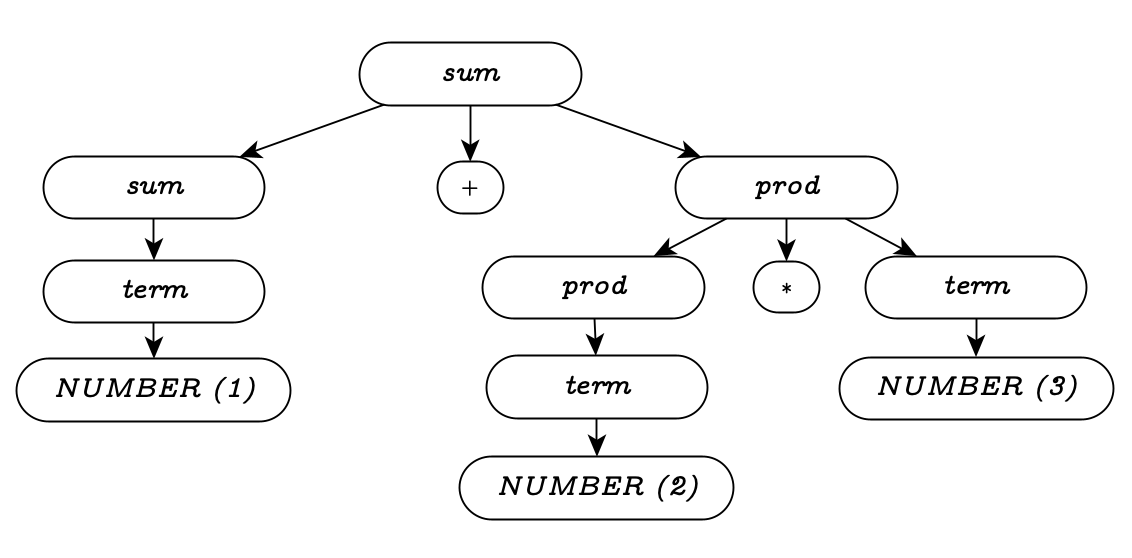
Eliminating Ambiguity

One way to eliminate ambiguity is to create an explicit precedence in how our operators apply. If we treat products as “lower-level” in the grammar than sums, we can ensure that they apply before sums do. (We’ll actually merge expr into sum for this example, because it makes for simpler trees)

sum:      prod
       |  sum  '+' prod

prod:     NUMBER
       |  prod '*' NUMBER

In this version of the grammar, we see that product non-terminals cannot contain sums, so all products are applied before any sums are generated. This preserves our familiar rules of arithmetic.

Shift-Reduce Parsers

With that understanding, we are in a position to describe hoc’s parser. Technically, it’s a shift-reduce LALR(1) parser. Let’s break that down.

LALR(1) stands for “lookahead-1, left-to-right”, which effectively says that we’ll always be able to decide which production to use by looking one token ahead.

Shift-reduce parsers build parse-trees from the “bottom-up”, and their name comes from how they operate. At each step, they have a “forest” (or stack) of subtrees that they have parsed, and a “next token” that they can examine. First, they check whether there is a nonterminal rule that matches the top nodes of their stack and is compatible with their next token. In that case, they reduce their forest by combining those nodes into a larger node. Eventually, they cannot reduce any further, and they instead shift the input token onto their stack, so that it can be used for later reductions.

Shift-Reduce Operation by Example

Let’s examine how a shift-reduce parser would handle the input 1+2*3, given our most-recent grammar.

To begin with, we have no stack at all, so we begin by shifting.

Now, our stack contains a NUMBER and our next token is a +; this matches only one production: sum '+' prod. So, we know that we must reduce our stack to create a sum, if possible. There is exactly one rule that reduces NUMBER symbols—the prod rule. We apply it to generate a prod on our stack.

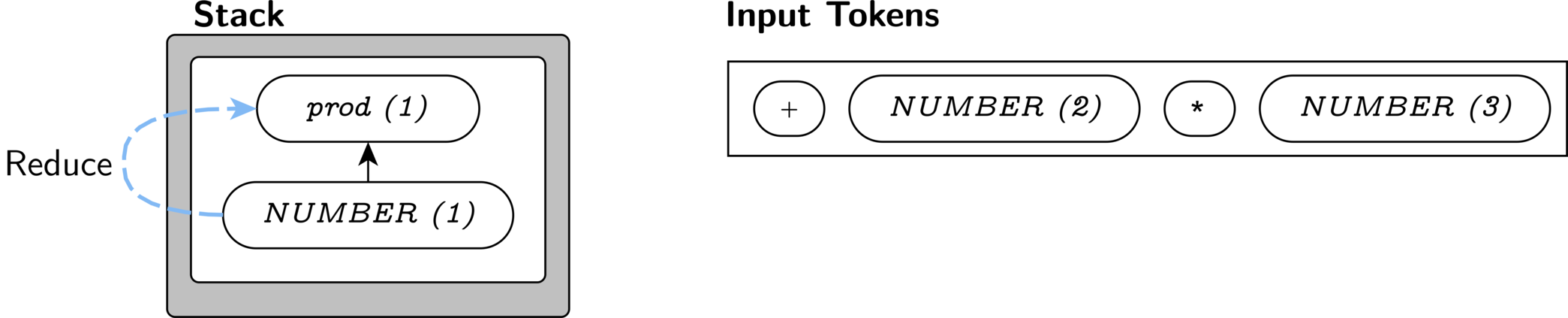
A prod can be directly reduced to a sum, so we reduce again to change our prod stack symbol into a sum stack symbol.

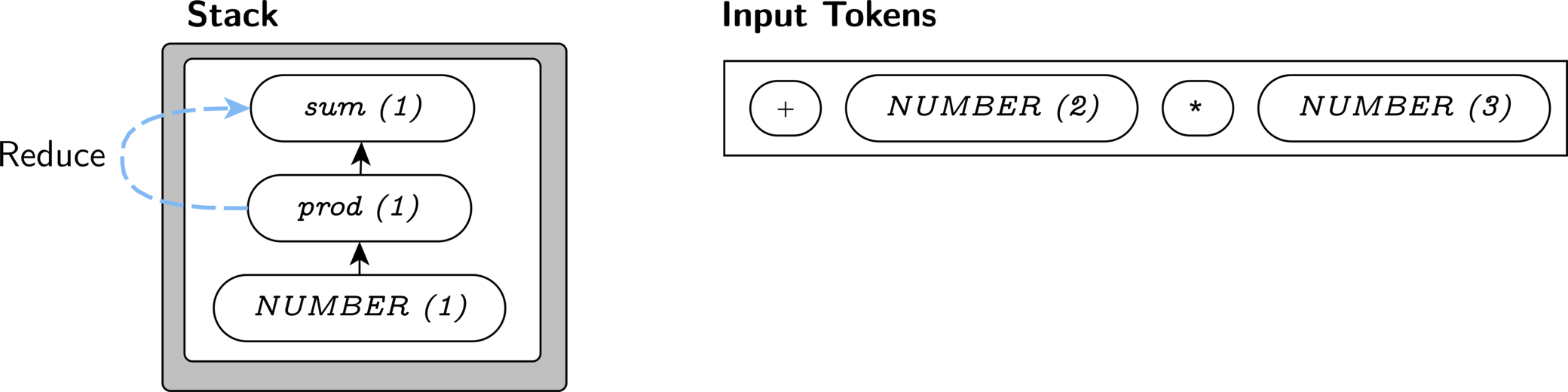
We cannot reduce any further, so we shift the +.

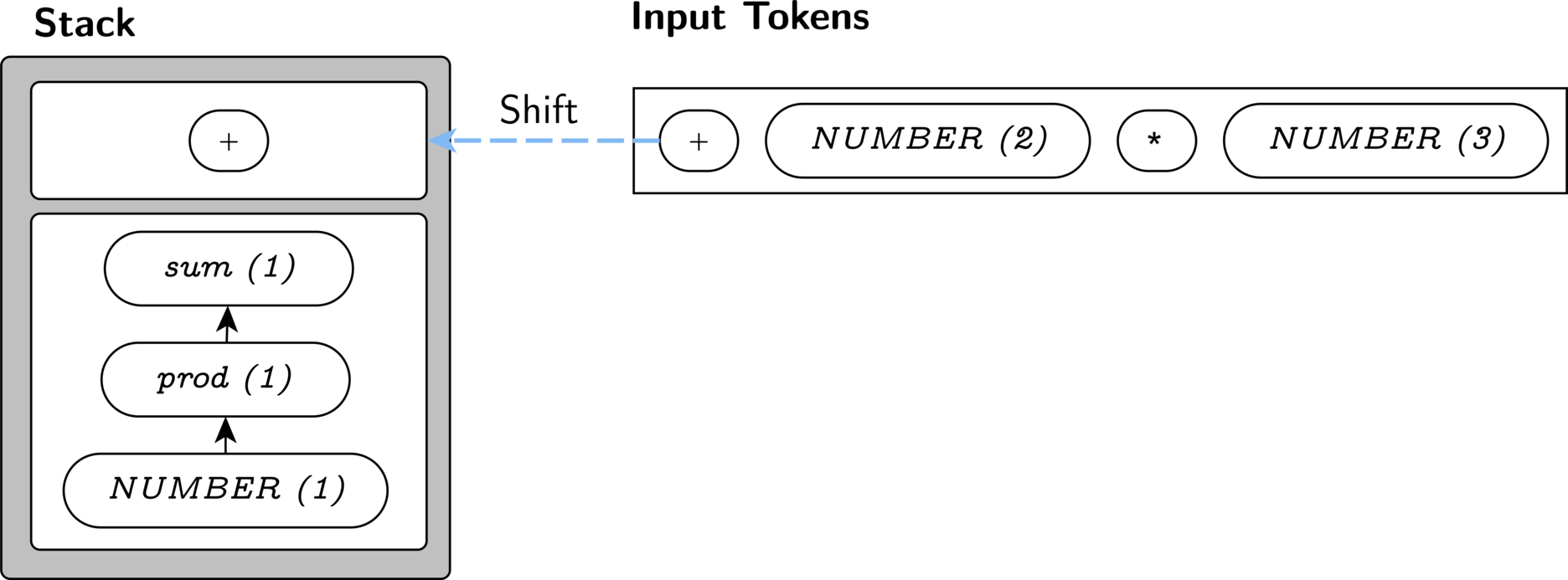
Similarly, we must shift the 2.

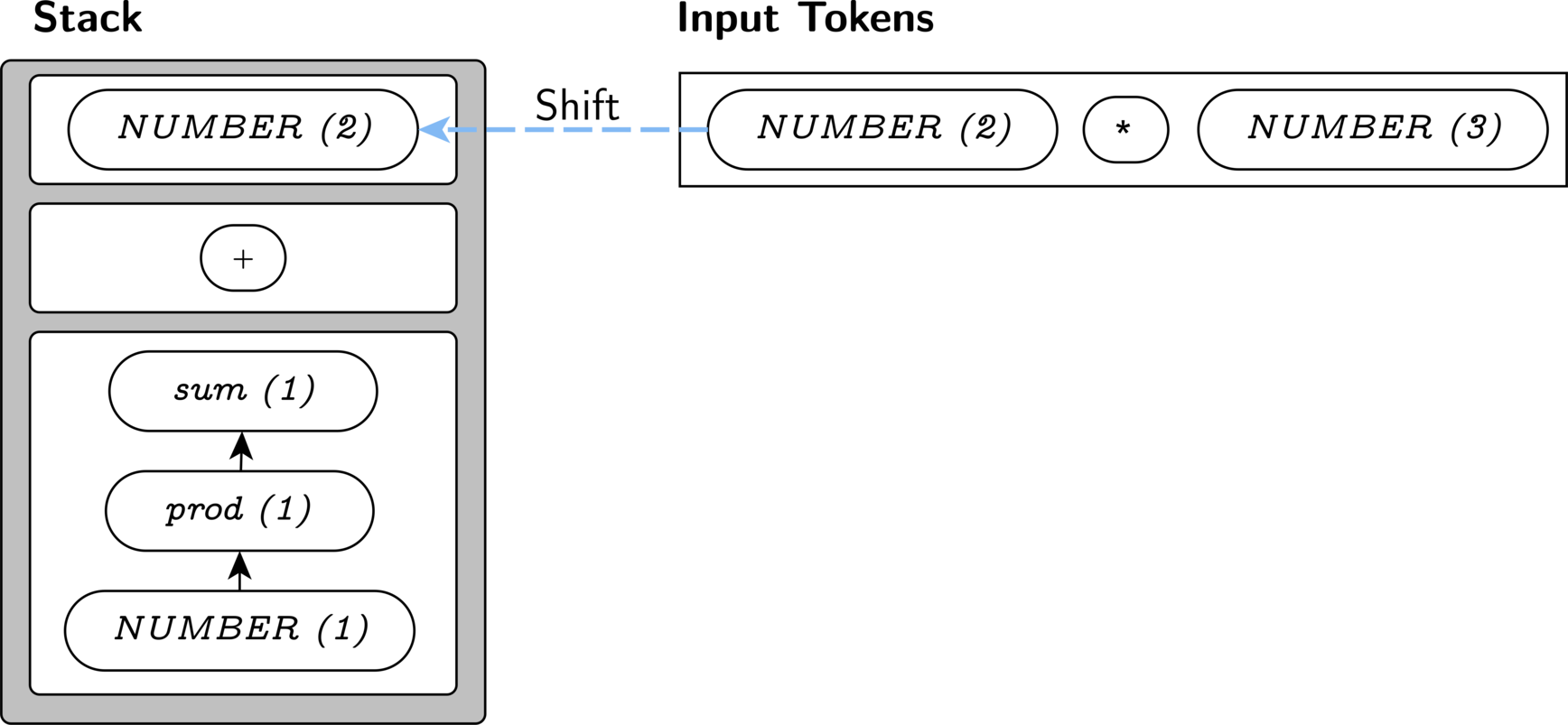
Our next input is *, which only matches prod '*' NUMBER. We are forced to reduce our NUMBER(2) to a prod, so that the next input token can be processed.

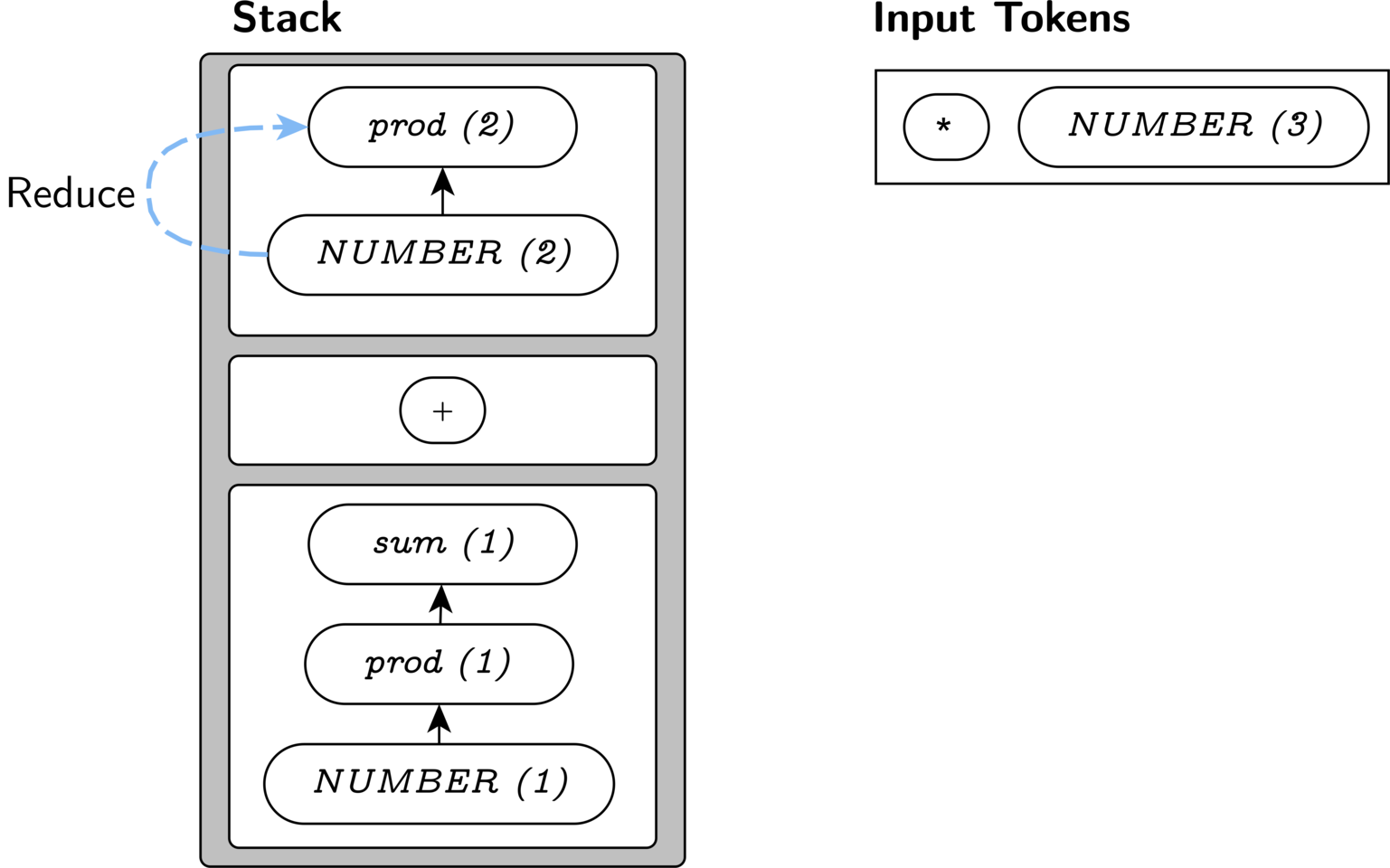
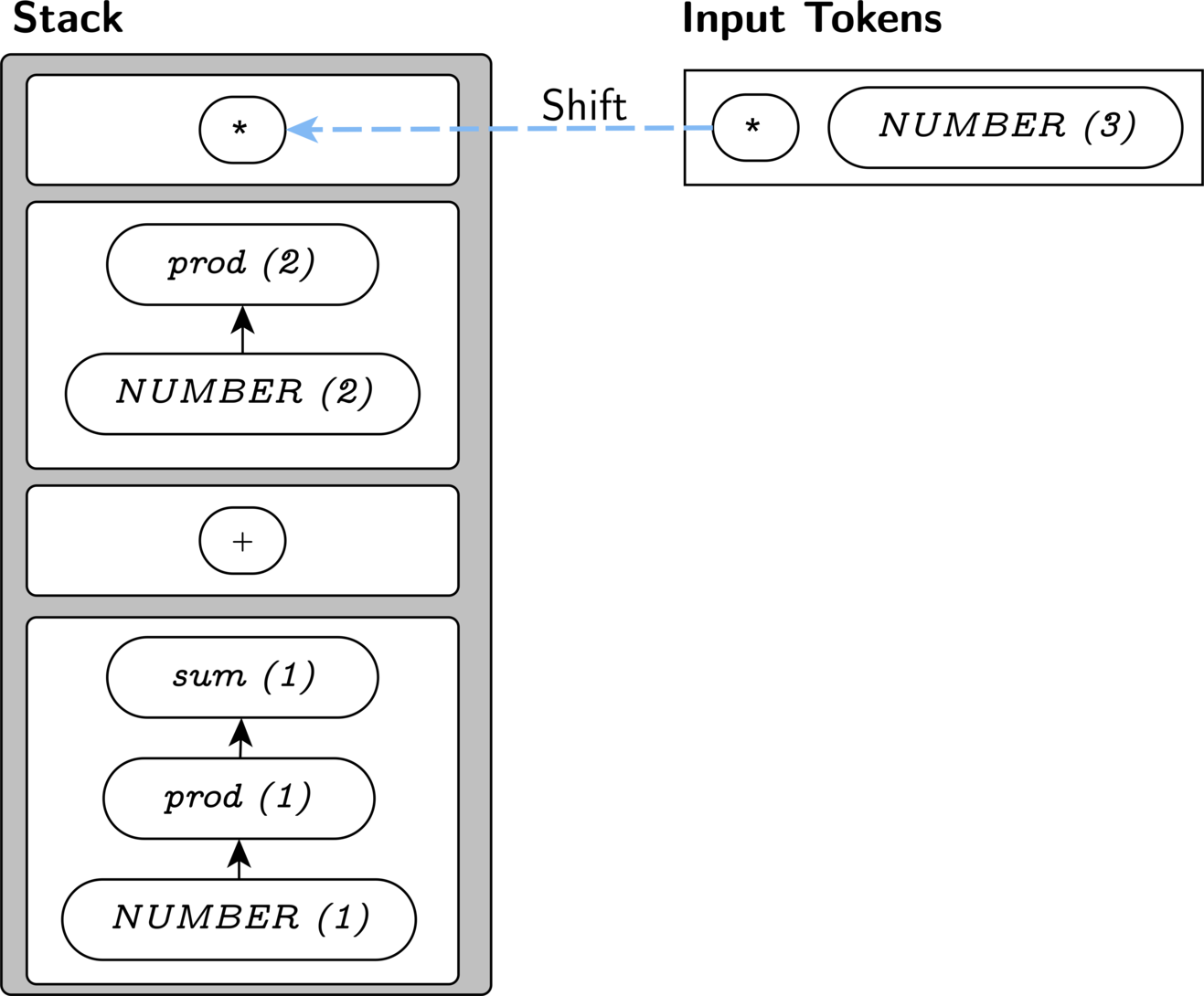
It might seem like we should again reduce our stack to a sum here, because the stack contains the appropriate symbols for the production it matches a valid production: sum: sum '+' prod. But we cannot, because there is no production matching the prefix sum *. Our lookahead token tells us that we must continue adding to the prod at the top of our stack. So, we shift here, since we do have a production for prod *.

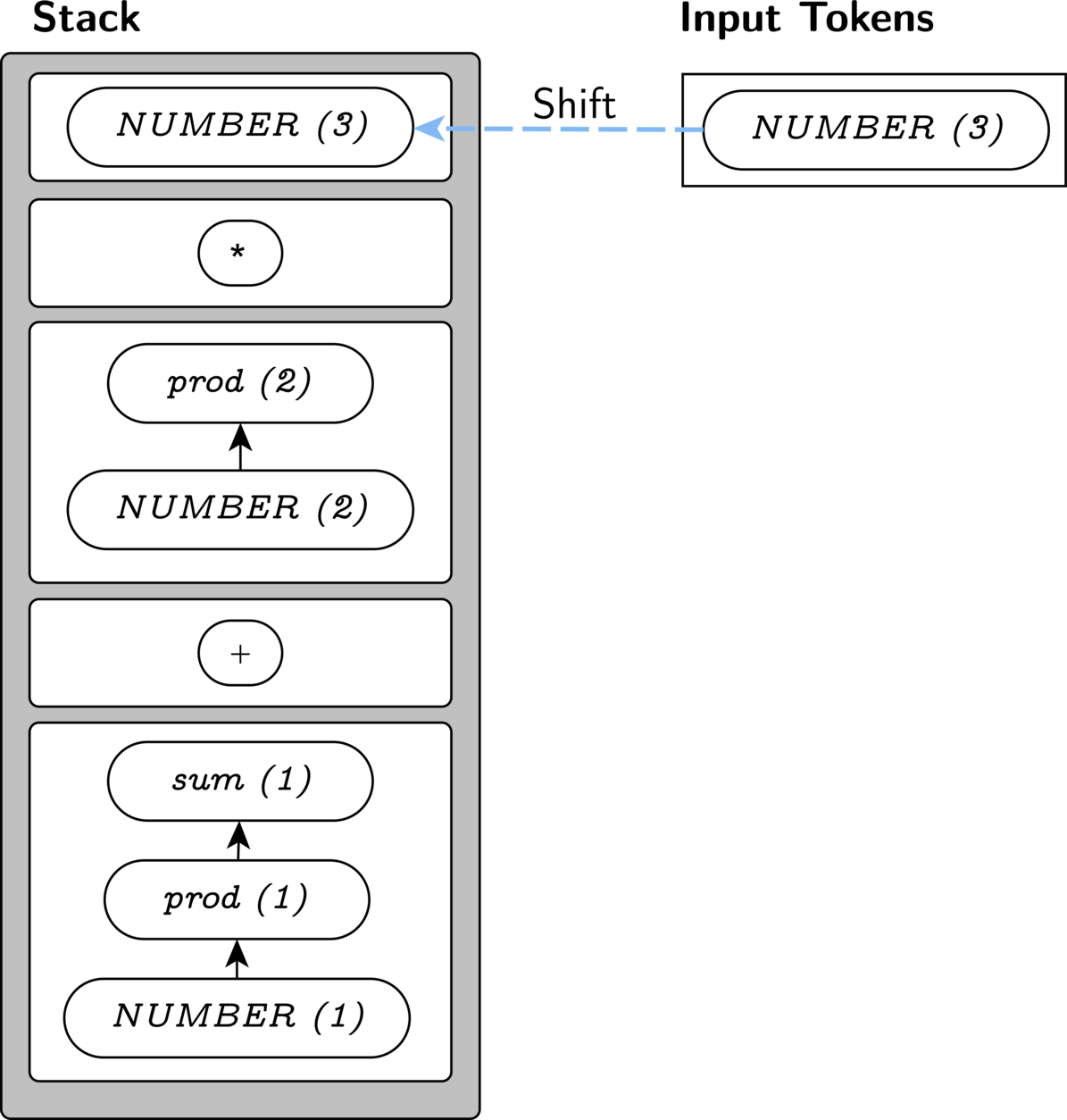
We know that we can prod * prod via a reduction from NUMBER(3) to prod, so we are allowed to shift NUMBER(3) onto the stack as well.

At this point, we proceed to make reductions from the top of the stack until one of two situations occurs:

1. We have only the start symbol left, and the parse completes successfully.
2. We run out of matching productions, and have an error.

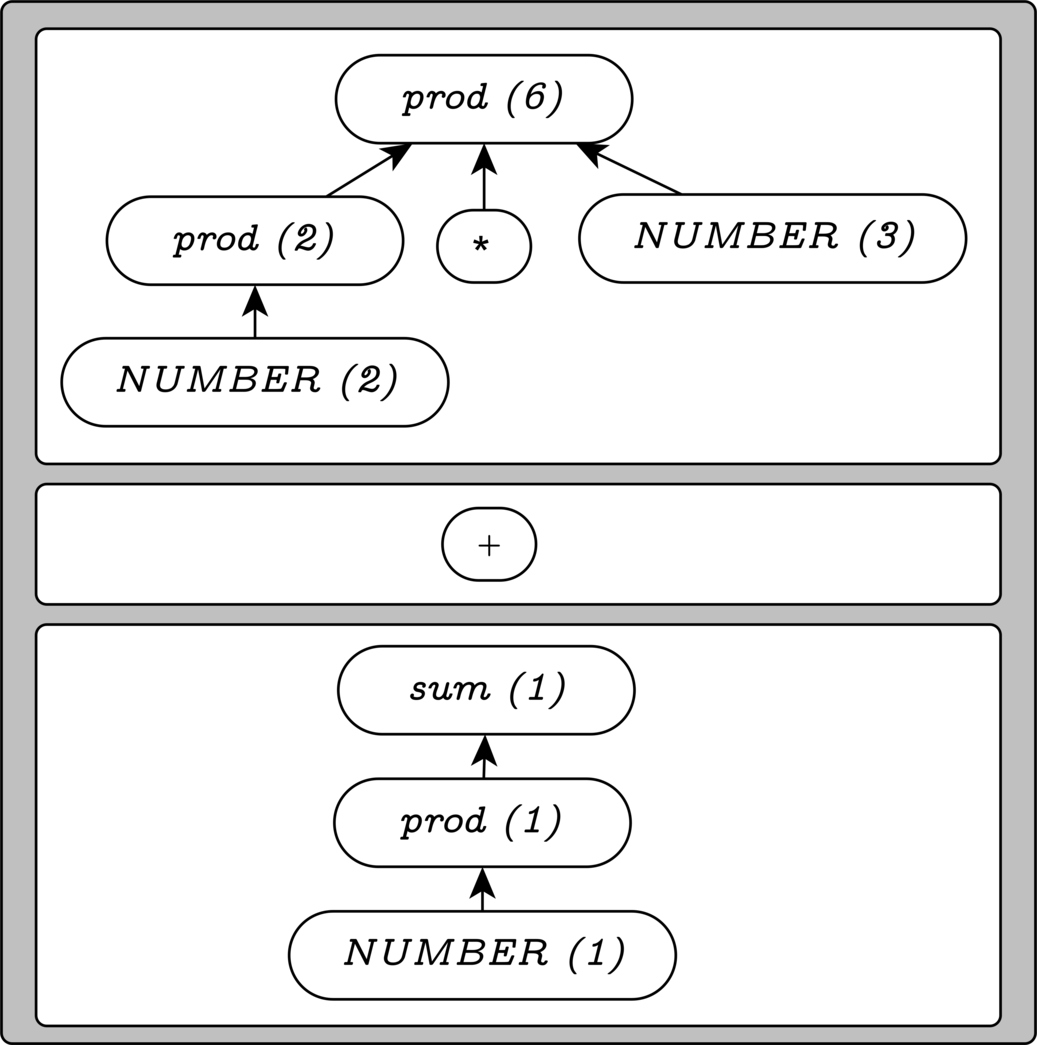
The top 3 items in our stack match the prod rule, reducing to another prod.

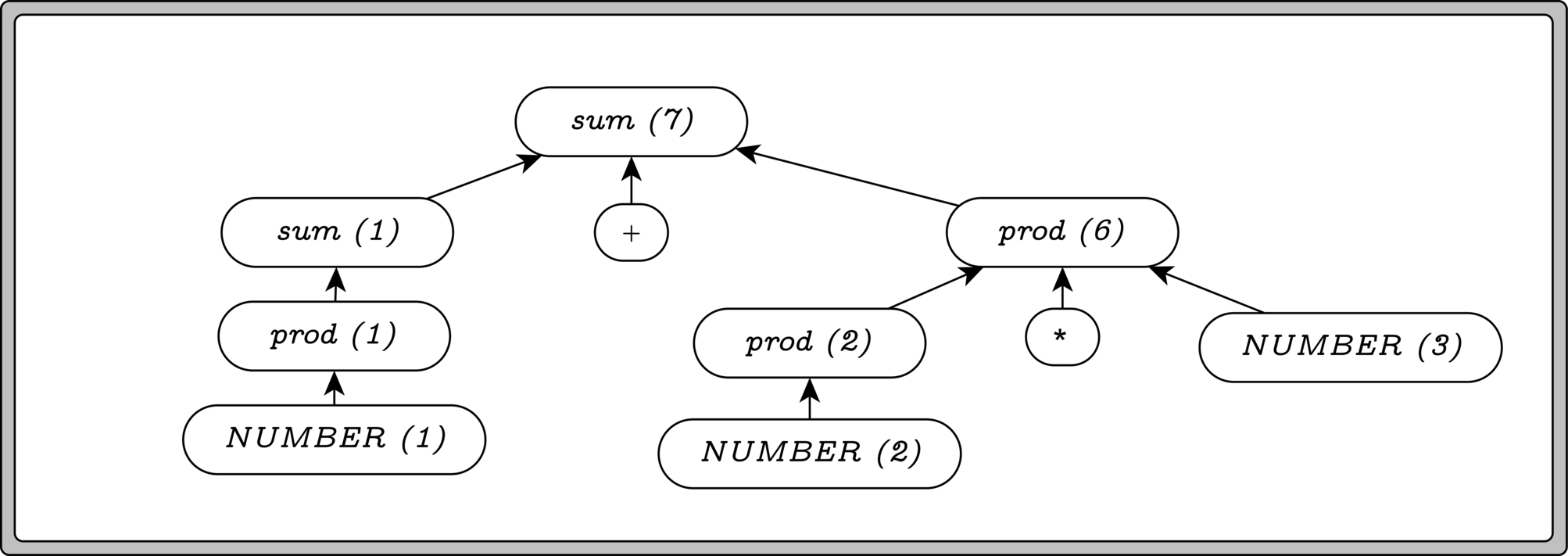
Finally, we can reduce sum + prod to a single sum, which is our start symbol. That’s all, folks!

Doing Something Useful: Parser Actions

This describes how a shift-reduce parser recognizes input data successfully, but what about that other important part? Producing a useful result or side-effect for our program?

A common way to add this functionality to a shift-reduce parser is to allow declaring actions that will run as part of the reduction steps of the algorithm. Each time a reduce occurs, the parser will perform an associated action, producing some useful value.

For example, let’s annotate our grammar with the actions we’d like to perform. Let’s assume that the values produced by the symbols in a rule are available as $1, $2, etc.

sum:      prod             { return $1; }
       |  sum  '+' prod    { return $1 + $2; }

prod:     NUMBER           { return $1; }
       |  prod '*' NUMBER  { return $1 * $3; }

Now, as each production is used to reduce our stack, it also produces a value. The result of the entire parse operation is the value produced by the start symbol. If you look back at the example from our previous section, you’ll see the values being produced in parentheses next to the root node of the trees.

Tokens have value too

If you look closely, the NUMBER tokens we receive during parsing also have a value associated with them. Associating the tokens with values is the responsibility of the component that’s tokenizing the input (the lexer).

Writing Parsers with yacc

Now, parsers are almost always written as a pipeline; our input is the user’s text, the output is our “useful result”, and in between, each stage receives the results of the prior stage. There can be an arbitrary number of stages, but we’ll almost always have the following two components:

1. A lexer (or tokenizer) - This component handles the work of normalizing raw user input and turning it into the tokens a shift-reduce parser needs. For programming languages, this stage also usually strips whitespace and comments.

2. Syntax Analyzer - This component does the work we’ve discussed up to now: matching tokens against our language rules, and producing some result.

Luckily, it turns out that once we’ve constructed a grammar for our language, building a parser is relatively straightforward; so much so that it can be automated! And that’s what yacc does for us: given a set of tokens, rules for our grammar, and (optionally) some actions in C that we want to perform, yacc generates a parser function for us.

Using yacc

The yacc program is run against a source file, and generates a parser function. Given a grammar and (optional) actions to perform for each production, it will create a C file with the implementation of a shift-reduce LALR(1) parser. The parser recognizes your language, and as each production is reduced, the associated actions will be performed. This is all implemented within a function called yyparse().

Using yacc is fairly simple, but adds an additional build step to our process. Instead of writing pure C code, we’ll write our parser program in a mixture of C code and a yacc grammar. We’ll pass that file to the yacc program (probably already installed on your machine), and it will generate a C file, which contains:

• All of our code
• A definition for a yyparse() function, which handles the details of parsing.

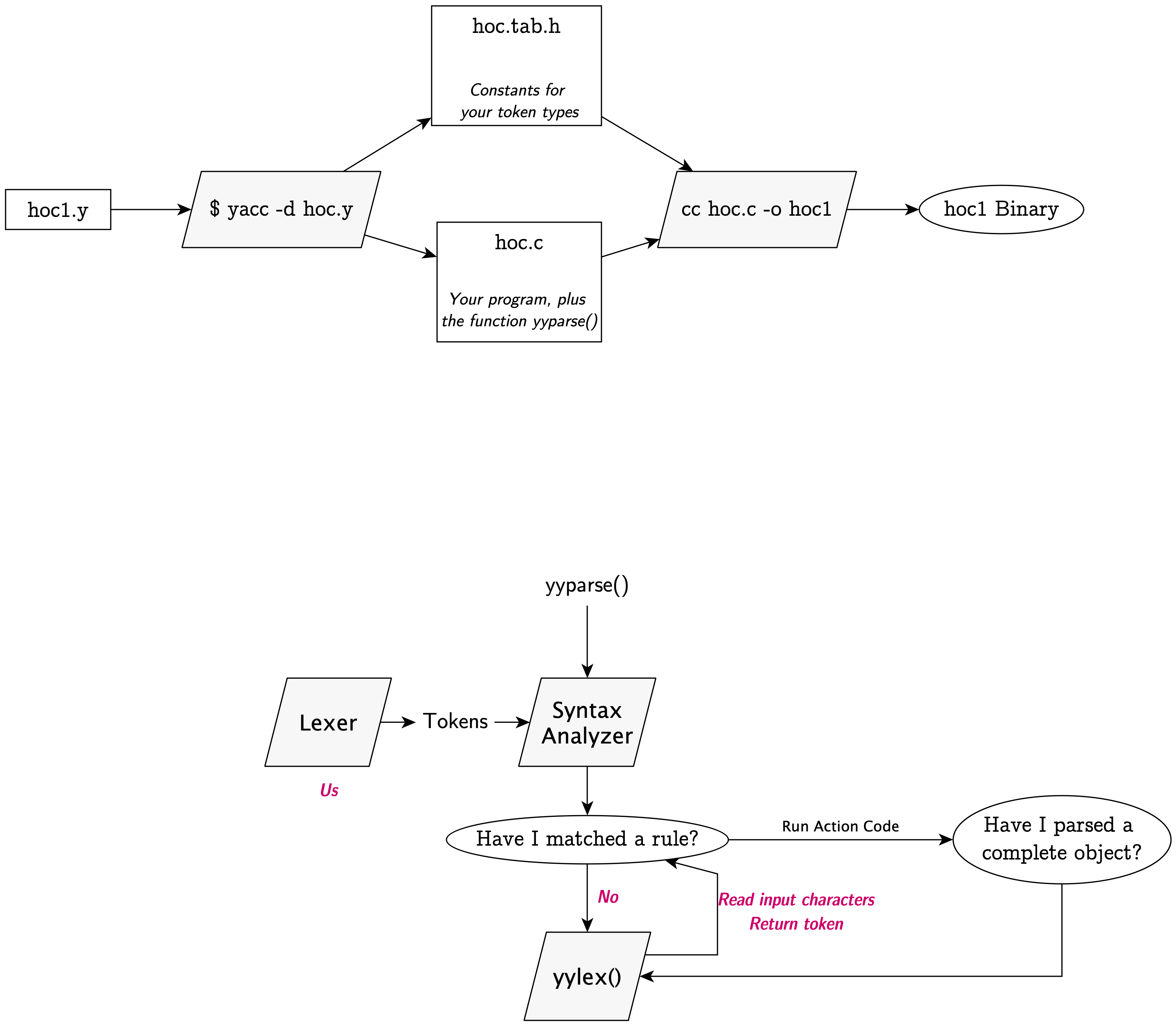
Our contract with yacc

A complete yacc file only needs its grammar and token definitions to generate its C file. However, as we’re compiling the generated yyparse() function, it will freely use two functions that must be available:

1. int yylex(void) - the lexer function, which is called to fetch the next token in the input.
2. void yyerror(const char *msg), which yylex will call when it finds a syntax error.

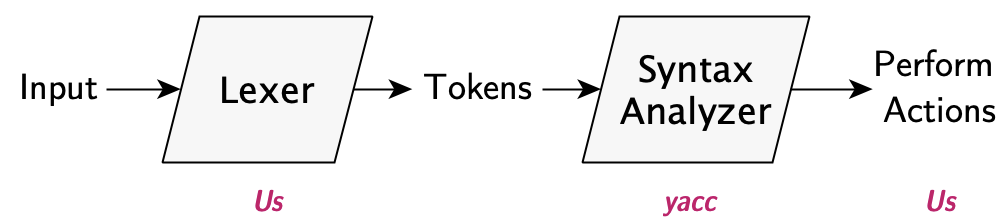
The hoc1 Parser

The hoc1 program is, first-and-foremost, designed as a line-by-line interpreter. Its interface is a REPL (Read-Eval-Print Loop), and its design reflects that; all of its logic starts from the language definition and actions of its input parser.

The components of hoc1 are:

• An input tokenizer, which reads user input from stdin and breaks it into tokens
• The yacc-generated parser, which executes our actions on each reduction
• An error-handling function, called by the parser when it can’t parse user input.

Once the user writes a line to stdin, the parser begins to request tokens from our lexer function. As it gets each token, the parser will perform the shift/reduce behavior we’ve described, following the productions we’ve defined.

In hoc1, all of our reduction actions either

1. Produce a arithmetic result
2. Display a result value

To understand how hoc1 works, we’ll look at:

1. The language it recognizes, including its tokens & productions
2. The lexer function for recognizing the tokens
3. The actions for each production
4. And lastly, the error handling any yacc parser requires

The structure of a yacc file

If you haven’t already, take a look at hoc1.y in the file browser (or, if you’re on mobile, you can open hoc1.y in another tab).

All yacc files have four sections, the first wrapped in brace-percent signs {% ... %}, and the other three separated by %% symbols:

%{ /* C prologue */ %}

/* Declarations:
 * yacc declarations, e.g. token types,
 * your produced types, etc. belong here
 */

%%

/* Grammar section: yacc grammar (rules, actions) */

%%

/* Epilogue: any C code required for parser can go here
 * For short programs, you may also *use* the parser here.
 */

1. C Prologue (a.k.a C Preamble) - Often, our language will be constructing or using types, objects, or values that we define. Obviously, we’ll need their declarations available, so our file may begin with an optional block of C code, which is added verbatim to the top of the generated output.

   This is also the place where we add any any necessary global state, forward declarations, and #include declarations necessary for the rest of the code.

2. Yacc Declarations section - Here, yacc requires us to define the token types and semantic values that we’ll use in our language grammar. The yacc-specific keywords all start with–you guessed it–"%". The hoc1 file contains just two: %token and %left, explained later.

3. Grammar section (Yacc-only) - This is where our grammar belongs, as well as any actions for our grammar rules.

4. Epilogue (C only) - The rest of our code, including our main() function, if any. This code gets to use yyparse().

Declarations and Types

First, let’s look at the C declarations we’ll need, and which yacc will output verbatim at the top of the generated file.

Our C preamble first #includes a couple of standard libraries, and forward-declares the subroutines that yyparse will call. If we left these out, yacc’s generated code will simply assume the functions exist and call them, leading to compiler warnings.

#include <stdio.h>
#include <ctype.h>

int yylex(void);
void yyerror(const char *s);

Our value type: The prologue also defines the YYSTYPE² macro, which tells yacc that all of our tokens will have the specified type.

If our grammar produces different values for different nonterminals, then we need a more complex declaration, but for hoc1, every nonterminal either produces no value or a double.

#define YYSTYPE double

%} // End preamble

hoc1’s yacc declarations

The yacc definitions include our token types; these are the “pieces” of the language that we’ll recognize and send to the parser from our lexer. We only have to declare tokens that take more than one character to represent; yacc handles single-character tokens like + or @ automatically. So long as our lexer simply returns those characters verbatim, yacc handles them.

Of course, our main token of importance is NUMBER, the token for a decimal number.

%token NUMBER

The rest of hoc1’s declarations exist to customize the behavior of our grammar, so we’ll discuss those in the next section.

The Grammar Section

The first version of hoc’s language is a list of expressions, one-per-line. An expression is simply a normal arithmetic expression. Empty lines are also allowed.

Format of a yacc production

Yacc productions look much like the CFG productions we’ve already defined, with one difference: the actions to perform during a reduction are specified in braces following the production’s rule.

%%
non_terminal:   symbol1 symbol2 .. symbolN
                {
                    // Your actions: This is just C code
                    // You can *produce* a value using the syntax below
                    $$ = <your return value>;
                }
         |      different-symbol1 different-symbol2...
                {
                    // a completely different action here
                }
         ; // production ends with (optional) semicolon

Notice that we produce a value from a reduction via the syntax

$$ = myReturnValue;

hoc1’s productions

In hoc1, our input defined as a “listing” - a set of zero or more lines. Each line contains a mathematical expression (expr). Thus, our grammar only has two nonterminals:: list and expr.

Recognizing Lists of Expressions

Recall that every grammar needs a start symbol; it is the root of our parse tree, and if we’ve produced that symbol upon reaching the end of our file, we’ve successfully parsed our input.

A common pattern in yacc interpreters is to define the start symbol so that it can match an infinite amount of input; this means that we’ll stop parsing only when the program exits.

This is exactly what hoc1 does, by treating the input as a set of “lines”, and each line is either empty, or is an expression. As we’ve seen, the list rule uses left-recursion to match multiple exprs.

%%
...
list:   /* nothing */
        | list '\n'
        | list expr '\n'    { printf("\t%.8g\n", $2); }
        ;

The only new feature is the very first production:

%%
list: /* nothing */

Because an empty list is allowed, the list \n production may match multiple times, and so the user may hit ⏎ as many times as they like before entering text again.

Recognizing Expressions (expr)

The productions of hoc should be somewhat familiar from our earlier expression grammars; notice that the values of nested expr nonterminals are available inside our actions as $1, $2, etc.

%%
...
expr:     NUMBER            { $$ = $1; }
        | expr '+' expr     { $$ = $1 + $3; }
        | expr '-' expr     { $$ = $1 - $3; }
        | expr '*' expr     { $$ = $1 * $3; }
        | expr '/' expr     { $$ = $1 / $3; }
        | '(' expr ')'      { $$ = $2; }
        ;

The only aspect of the grammar that may seem strange is its brevity: it seems like it should be completely ambiguous!. In fact, yacc provides mechanisms for resolving ambiguities that we can use to keep our grammar smaller.

How yacc determines precedence of a production

Unlike a plain context-free grammar, which has no mechanism to specify the precedence of one symbol or production over another, yacc allows us to explicitly assign a precedence to any token.

This also implicitly defines the precedence of our productions, because the precedence of a production rule is set to the precedence of the rightmost token in that rule.

So, while we could have split our definition for expr into multiple productions, as we did above:

%%
expr:     prod
        | expr '+' prod
        | expr '-' prod

prod:     term
        | prod '*' term
        | prod '/' term

term:     NUMBER
        | '(' expr ')'

Instead, we can simply assign a higher explicit precedence to the * and / tokens than to + and -.

Now, token precedence is set by their order in the file: lower-priority tokens are placed before higher-priority ones.

You might think we’d declare the tokens with the token keyword, but this doesn’t actually help. Historically, yacc had an odd quirk: it used the order of the token’s associativity declarations to determine their precedence! (This is due to the fact that you rarely need one without the other).

So, we’ll inform yacc that our operations are left-associative, and it will then use the order of the lines to determine precedence. Tokens with the same precedence should be placed on the same line, and then they’ll be parsed left to right. We add this information near our token declarations, in the yacc declarations section.

%left  '+' '-' /*  left-associative, same precedence */
%left  '*' '/'  /* left-assoc; higher precedence */

Our Actions

These are specified in curly braces with each production. As we’ve seen, most of our actions simply produce a value by assigning it to the special variable $$. Yacc will automatically push that value onto its stack, and we can use it in later rules that might use our non-terminal. So long as our lexer produces a double value when it recognizes NUMBER tokens, we’ll produce correct results.

Once a newline is matched, the list action will run and print its result.

The hoc1 Lexer

Before we can parse anything, we must split our input into tokens. Since the tokens for hoc are all relatively simple, we do this “by hand”, reading a character at a time, performing some additional processing if we recognize it, and passing it on otherwise.

Our yylex function has two jobs:

1. Return the token type we recognize; either the character literal (e.g. '+' or '*') or a constant such as NUMBER.
2. If the token has a value, which NUMBER tokens do, set that value to yylval; these values are made available to actions.

First, we perform the classic lexer task: skipping whitespace.

int yylex(void) {
    int c;
    do { // skip spaces
        c = getchar();
    } while (c == ' ' || c == '\t');

Finally, we have reached a non-whitespace character. There are only a few options for how we’ll handle it. Firstly, any EOF character should be reported to the parser right away, since we’re done parsing.

    if (c == EOF) {
        return 0;
    }

If instead we’ve found a digit or decimal, then we have a NUMBER token! To find its complete value, we push the character back onto the input stream and use scanf to get the number for us. The value of the number gets placed into the yylval variable.

    if (c == '.' || isdigit(c)) {
        ungetc(c, stdin);
        scanf("%lf", &yylval);
        return NUMBER;
    }

Producing token values: yylval

Some token types, like \n, don’t have a meaningful value; those are easy to signal by just returning the token itself. But for tokens with a type and a value, like NUMBER, we need to signal to the parser that a value is available. Unlike our actions, yacc does not control our lexing code, so we cannot assign to the $$ variable. Instead, yacc provides yylval, or Lexer Value. This is a global variable that yylex is allowed to modify. Whenever we refer to the value of a token in our actions, yacc just rewrites that reference to point to yylval.

So, whenever we have a token with an associated value, we perform two actions:

1. Return the token type: the type of the token, e.g. NUMBER, should be returned from the lexer.

2. Store the token value in the yylval variable

Finally, we increment a line number if one’s seen, and, since no other behavior was triggered, we return the literal character we read:

    if (c == '\n') {
        line_number++;
    }

    return c;
}

Notice that, as promised, we don’t need any handling in our lexer for the arithmetic operators or parentheses; their character values are returned directly. When tokens are defined as literal characters, returning those literals from yylex is valid behavior, and they’ll be recognized. If the character we return is not recognized as one of our %token declarations, then an error will be reported.

Our Error Reporter: yyerror()

When yyparse discovers input that it does not recognize, it reaches an error state. At this point, the yyerror(const char *msg) function will be called.

This function is called by yacc when it discovers a syntax issue in the input. It’ll be called with a message from yacc describing the error it discovered; this will almost always just be the string "syntax error". Our hoc1 reporter is self-explanatory:

void yyerror(const char *s) {
  fprintf(stderr,
    "%s: %s (on line %d)\n",
    program_name, s, line_number);
}

Unfortunately, since a syntax error causes the parse to fail, this will also quit the application. We’ll fix this unfortunate behavior in hoc2.

Putting it all together: main() function

Since hoc1 keeps almost all program logic inside its “parser actions”, our main function is as simple as calling the yyparse() function generated by yacc. It’ll parse input until it gets an error or EOF.

int main(int argc, char *argv[]) {
    program_name = argv[0];
    return yyparse();
}

What’s Next

Whew! There are a lot of concepts introduced in hoc1, and all of them will continue to be useful throughout the rest of the series. I tried to include everything you need, with nothing you didn’t; that being said, there’s so much more to learn!

For more information on shift-reduce parsing theory and practice, as well as the algorithms behind yacc, see the seminal paper by Aho and Johnson.

If you want more information about yacc & its modern successor, see the Bison manual for more examples and discussion. It’s worth noting that their first examples closely mirror the shape of hoc, though I admit I don’t know who influenced whom.

Regardless, if you’re new to yacc, then I’d recommend spending some time playing with hoc1’s grammar at this point, to see if the theory makes sense when faced with a real grammar. Perhaps you can add your own operators, or support for negative numbers (we’ll do both of these in hoc2 as well).

Once you’re comfortable with it, we can move on to hoc2, which is blessedly simple to understand now that we have our footing beneath us.